| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- n과 m
- 재귀
- REST
- streamlit
- 1002
- 경사하강법
- 오블완
- end to end
- 손실함수
- 밑바닥부터 시작하는 딥러닝
- pyenv
- 9020
- 신경망 학습
- 15649
- 가상환경
- 티스토리챌린지
- 백준
- REST API
- N-Queen
- 백트래킹
- 개발환경
- 그리디 알고리즘
- Python
- 기계학습
- 1101
- 실버
- 파이싼
- 파이썬
- BOJ
- 4948
- Today
- Total
파이톨치
[부스트캠프] 인공지능 기초 다지기 - 기초 수학 - 확률론 본문
확률론
인공지능 분야에서 확률론과 딥러닝의 관계는 여러 가지 이유로 중요합니다:
불확실성 모델링: 현실 세계에서 데이터와 문제는 종종 불확실성을 내포하고 있습니다. 확률론은 이러한 불확실성을 효과적으로 모델링하고 다룰 수 있는 수학적 도구를 제공합니다. 딥러닝 모델 역시 확률적으로 출력을 내는 경우가 많고, 이를 통해 모델의 불확실성을 추정하거나 관리할 수 있습니다.
통계적 학습 이론: 확률론은 통계적 학습 이론의 기초를 제공합니다. 학습 데이터로부터 모델을 학습시킬 때, 데이터가 표본일 뿐인데 이를 바탕으로 일반화된 패턴이나 결정을 내리기 위해 확률론적 접근이 필요합니다. 특히, 작은 데이터셋이나 노이즈가 많은 데이터에서 모델을 효과적으로 학습시키기 위해 확률론적 방법이 중요합니다.
베이지안 추론: 베이지안 추론은 확률론적 사고의 중요한 한 축입니다. 이는 주어진 데이터를 토대로 모델의 불확실성을 감안하여 추론하는 방법론을 말합니다. 딥러닝에서도 베이지안 방법론을 적용하여 모델의 불확실성을 추정하거나 추론 과정에서 확률적으로 접근할 수 있습니다.
기초 확률 개념
평균
확률론에서의 평균은 주어진 확률 변수의 값들의 기댓값을 의미합니다. 확률 변수 X가 확률 분포를 따를 때, 그 평균은 다음과 같이 정의됩니다:

이는 확률 변수 X의 각 값 x가 발생할 확률을 그 값 자체와 곱한 후 모두 합산하여 구합니다.
분산
분산은 확률 변수의 값들이 평균에서 얼마나 멀리 흩어져 있는지를 나타내는 측도입니다. 수식적으로는 다음과 같이 정의됩니다:
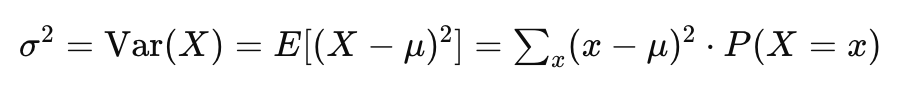
분산은 확률 변수의 각 값과 평균의 차이를 제곱하여 그 확률에 가중치를 주어 합산한 값입니다. 분산의 양이 클수록 데이터가 평균에서 멀리 흩어져 있음을 의미합니다.
표본 분산은 실제 데이터 샘플들을 바탕으로 계산되는 분산입니다. 주어진 데이터 샘플 에 대한 표본 평균 을 구한 후, 각 데이터 값과 표본 평균의 차이를 제곱하여 평균을 취한 값입니다:
표본 분산에서 로 나누는 이유는 데이터가 모집단에서 추출된 표본일 경우, 모집단의 분산을 추정하는 데 정확성을 높이기 위한 보정입니다.
X={1,2,3,4,5} 가 표본 일 때, 평균은 3이고 표본 분산은 (4+1+0+1+4) / 4이다. 즉, 10/4 이며 2.5이다.
조건부 확률
조건부 확률은 어떤 사건이 다른 사건이 일어난 조건 아래에서 발생할 확률을 말합니다. 보통 로 표기하며, 이는 사건 B가 일어났을 때 사건 A가 일어날 확률을 나타냅니다. 수식적으로는 다음과 같이 정의됩니다:

독립 사건인 경우, P(A⋂B)=P(B∣A)P(A)=P(B)P(A)가 된다. 두 사건의 곱으로 연산된다.
베이즈 정리
베이즈 정리(Bayes' theorem)는 조건부 확률을 계산하는 유용한 정리로, 머신러닝, 통계학, 확률론 등 다양한 분야에서 활용됩니다.
베이즈 정리는 사전 확률(prior probability)과 사후 확률(posterior probability) 사이의 관계를 나타내며, 새로운 정보가 주어졌을 때 이를 통해 사건의 확률을 업데이트하는 데 사용됩니다.
조건부 확률 P(A∣B)는 사건 B가 발생한 경우 사건 A가 발생할 확률을 나타냅니다. 베이즈 정리는 이를 다음과 같이 표현합니다:

여기서 각 항은 다음을 의미합니다:
- P(A∣B): 사건 B가 발생한 조건에서 사건 A가 발생할 확률 (사후 확률, posterior probability)
- P(B∣A): 사건 A가 발생한 조건에서 사건 B가 발생할 확률 (가능도, likelihood)
- P(A): 사건 A가 발생할 확률 (사전 확률, prior probability)
- P(B): 사건 B가 발생할 확률 (정규화 상수, marginal likelihood 또는 evidence)
예시 1) 한 학급에 학생이 100명이 있다. 여학생 30% 중 3%가 외국인이다. 또 남학생 70% 중 8%가 외국인이다. 해당 학급에서 임의로 뽑은 1명이 외국인일 때, 이 학생이 여학생일 확률을 구하시오(소수점 셋째자리에서 반올림 하시오).
P(여학생 | 외국인) ?
P(외국인 | 여학생) = 0.03
P(외국인) = 0.3 * 0.03 + 0.7 * 0.08
P(여학생) = 0.3
P(여학생 | 외국인) = P(외국인 | 여학생) * P(여학생) / P(외국인)
인과관계
인과관계를 파악하기 위해서는 다른 요인들이 결과에 미치는 영향을 제거해야 합니다. 중첩요인이란 결과에 동시에 영향을 미칠 수 있는 요인을 말하며, 이를 제거하지 않으면 실제 원인과 무관한 요인들이 결과와 관련된 것처럼 보일 수 있습니다. 따라서 정확한 인과관계를 파악하기 위해서는 중첩요인의 효과를 제거해야 합니다.
중첩요인을 제거하지 않으면 실제로는 상관 관계가 없는 두 변수 간에도 연관성이 나타날 수 있습니다. 이를 가짜 연관성이라고 하며, 데이터 분석에서 잘못된 결론을 도출하게 됩니다. (예를 들어, 여름철 상어 사고율과 아이스크림 판매량의 상관관계)
인과관계를 이해하면 데이터 분포가 변화해도 예측 모형이 강건하게 유지될 수 있습니다. 원인과 결과 사이의 정확한 관계를 이해하면 예측 모형이 더욱 정확하고 신뢰할 수 있게 됩니다. 하지만, 인과관계를 이해하는 것만으로는 예측 정확도가 높은 모델을 만들기 어렵습니다. 인과관계 외에도 데이터의 다양한 요인들을 고려하여 모델을 구성하고, 데이터에 적합한 통계적 기법과 머신러닝 알고리즘을 적용해야 예측 정확도를 높일 수 있습니다.
데이터가 많아져도 조건부 확률만 가지고 인과관계를 추론하는 것은 불가능합니다. 왜냐면 가짜 연관성이 있기 떄문이다.
'AI&ML' 카테고리의 다른 글
| [부스트캠프] 인공지능 기초 다지기 - 딥러닝 - Layer (1) | 2024.07.03 |
|---|---|
| [부스트캠프] 인공지능 기초 다지기 - 딥러닝 - PyTorch (1) | 2024.07.03 |
| [부스트캠프] 인공지능 기초 다지기 - 기초 수학 - 벡터 (1) | 2024.07.03 |
| [CVPR 2022 tutorial] unified image-text modeling (0) | 2024.04.03 |
| [코드리뷰] Falmingo (0) | 2024.04.02 |


