| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 신경망 학습
- 경사하강법
- N-Queen
- 손실함수
- 가상환경
- streamlit
- 1002
- 기계학습
- 백준
- pyenv
- 파이싼
- n과 m
- BOJ
- 15649
- 재귀
- 4948
- 실버
- 설정
- 1101
- 밑바닥부터 시작하는 딥러닝
- 파이썬
- 백트래킹
- Python
- 9020
- Mac
- 개발환경
- end to end
- 그리디 알고리즘
- Today
- Total
파이톨치
인공지능 본문
인공지능이란 강인공지능과 약인공지능이 있다.
강인공지능의 경우에는 사람과 같은 지능을 말한다.
마음을 가지고 사람 처럼 느끼며 행동하는 인공지능을 말하는데
이러한 인공지능은 튜링테스트로 구분한다고 한다.
약한 인공지능은 특정 문제를 해결하는 지능적 행동을 한다.
흉내만 낼 수 있는 수준으로 깊은 이해를 하고 행동하는 것이 아니다.
중국인 방 사고 실험[존 설이 제시한 실험으로 중국어를 모르는 사람이지만
메뉴얼을 참조하여 답변을ㄹ 보내는 것이다. 이해하고 있다고 생각할 수 있지만
흉내만 내고 이해한 것이 아니다.]으로 이를 구분한다.
수단목표분석 : 블럭이동문제, move(c, table)
문제를 state로 정의하고 현재 상태와 목적 상태 간의 차이를 계산한다.
목적 상태 도달을 위해 조작자를 선택/적용하는 과정을 반복한다.
인공지능의 주요 응용분야는 [자연어처리, 컴퓨터 비전, 음성인식, 로보틱스, 에이전트] 등이 있다.
공간을 모두 찾아볼 수 없어서 탐색을 한다.
-- 맹목적 탐색 --
[상태 공간 그래프 문제] : 선교사-식인종 문제가 있다.
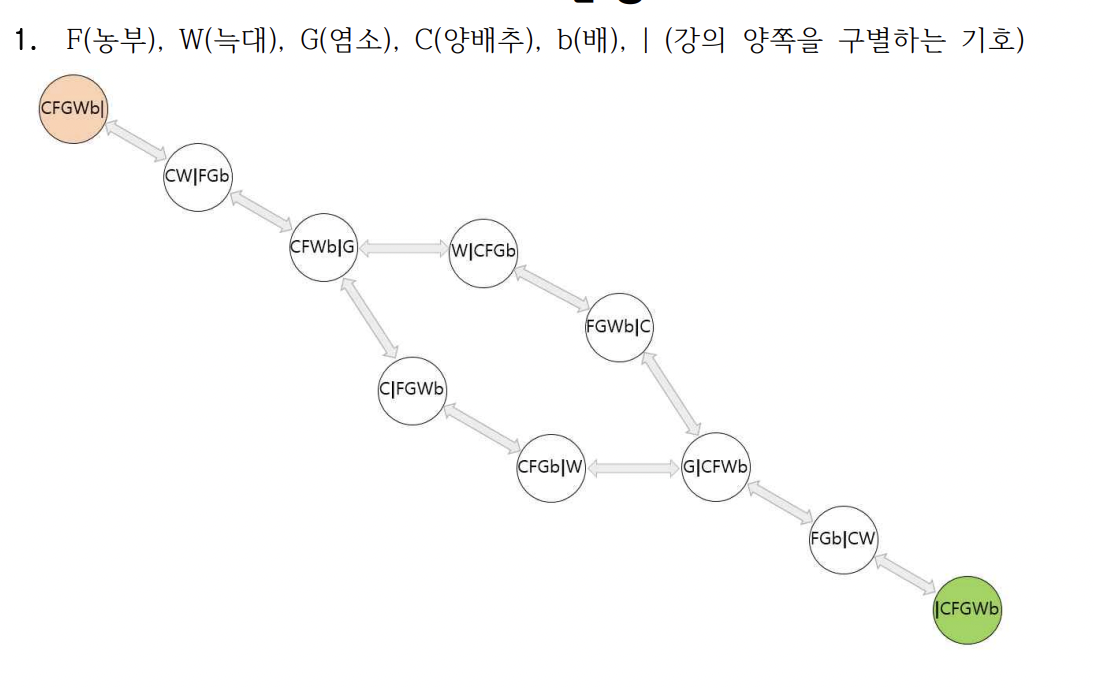
[깊이 우선 탐색] : 백트래킹, 도달하면 종료, 재방문 없음, 하나의 경로 유지
[너비 우선 탐색] : 모든 자식 노드 확장 -> 반복, 항상 최적해를 찾을 수 있음
# open 리스트
open_queue = [ ]
open_queue.append(State(puzzle, goal))
closed_queue = [ ]
moves = 0
# 디버깅을 위한 코드
#print("START OF OPENQ")
#for elem in open_queue:
# print(elem)
#print("END OF OPENQ")
while len(open_queue) != 0:
current = open_queue.pop(0) # OPEN 리스트의 앞에서 삭제
print(current)
if current.board == goal:
print("탐색 성공")
break
moves = current.moves+1
closed_queue.append(current)
for state in current.expand(moves):
if (state in closed_queue) or (state in open_queue): # 이미 거쳐간 노드이면
continue # 노드를 버린다.
else:
open_queue.append(state) # OPEN 리스트의 끝에 추가[반복적 깊이심화 탐색] : 깊이 한계가 있는 깊이 우선 탐색을 반복 적용, 너비 보단 적은 메모리, 최단 경로해 보장
하지만 깊이 우선보다는 비효율적인 메모리
[양방향 탐색] : 근본 없는듯
-- 정보 이용 탐색 --
[휴리스틱] : 신속하게 어림짐작하는 것이다.
[최단 경로 문제] : 현재 위치에서 목적지까지 거리
[8퍼즐 문제] : 제자리 x 타일 개수
[8퀸 문제] : 충돌 횟수
[언덕오르기방법] : 지역 탐색, 휴리스틱 탐색 -> 이웃 확장, but 국소 최적해 위험
[최상우선탐색] : 남은 거리가 가장 짧은 노드 확장
[빔 탐색] : 일정 개수의 확장 가능 노드만 관리 -> 최상우선탐색
[A* 알고리즘] : f(n) = g(n) + h(n)
# f(n)을 계산하여 반환한다.
def f(self):
return self.h()+self.g()
# 휴리스틱 함수 값인 h(n)을 계산하여 반환한다.
# 현재 제 위치에 있지 않은 타일의 개수를 리스트 함축으로 계산한다.
def h(self):
return sum([1 if self.board[i] != self.goal[i] else 0 for i in range(8)])
# 시작 노드로부터의 경로를 반환한다.
def g(self):
return self.moves
def __eq__(self, other):
return self.board == other.board
# 상태와 상태를 비교하기 위하여 less than 연산자를 정의한다.
def __lt__(self, other):
return self.f() < other.f()
def __gt__(self, other):
return self.f() > other.f()-- 게임에서의 탐색 --
[게임트리] : 상대방이 있는 게임에서 자신과 상대방의 가능한 게임상태, 많은 수를 볼 수록 유리함.
[mini-max 알고리즘] : max -> 나에게 유리한 값 선택, min -> 상대방이 유리한거 선택 -> 반복 -> 좋은거 선택
자신이 max가 되어야겠지
def minimax(board : list, depth : int, maxPlayer : int):
pos = -1
if depth == 0 or len(empty_cells(board)) == 0 or game_over(board):
return -1, evaluate(board)
# empty index에 해당하는 p일 경우 재귀를 통해 앞으로 이어질 경기를 예상하면서 최선의 수를 찾는다.
if maxPlayer:
value = -10000
for p in empty_cells(board):
board[p] = 'X'
x, score = minimax(board, depth-1, False)
board[p] = ' '
if score > value:
value = score
pos = p
else :
value = +10000
for p in empty_cells(board):
board[p] = 'O'
x, score = minimax(board, depth-1, True)
board[p] = ' '
if score < value:
value = score
pos = p
return pos, value[알파 베타 가지치기] : 검토해 볼 필요 없는 부분 탐색 안 하기
알파 자르기 -> min노드 현재값이 부모노드 현재 값보다 작거나 같으면 중지 [min(위) - max(아래)]
베타 자르기 -> max노드 현재 값이 부모노드 현재 값보다 같거나 크면 중지 [max - min]
** 뭐가 들어가도 결과가 같으면 잘라버리자. **
[몬테카를로 시뮬레이션] : 확률 분포 -> 무작위 표본 -> 행동 -> 반복
[몬테카를로 트리 탐색] : 트리 정책 + 기본 정책(시뮬레이션)
선택[UCB: 승률과 방문횟수(시도해본 횟수가 적은 노드를 선호) 고려] ->
-> 확장[트리정책] ->
-> 시뮬레이션[몬테카를로 시뮬레이션: 탐색 공간 축소] ->
-> 역전파[승점 반영]
알파고는 반복해서 형세판단함.
-- 제약조건 만족 문제 --
-- 유전 알고리즘 --
1. 후보해 표현 -> 염색체 표현함.
# 염색체를 클래스로 정의한다.
class Chromosome:
def __init__(self, g=[]):
self.genes = g.copy() # 유전자는 리스트로 구현된다.
self.fitness = 0 # 적합도
if self.genes.__len__()==0: # 염색체가 초기 상태이면 초기화한다.
i = 0
while i<SIZE:
if random.random() >= 0.5: self.genes.append(1)
else: self.genes.append(0)
i += 12. 모집단 : 동시에 존재하는 염색체들의 집합
# 초기 염색체를 생성하여 객체 집단에 추가한다.
while i<POPULATION_SIZE:
population.append(Chromosome())
i += 13. 적합도 함수
def cal_fitness(self): # 적합도를 계산한다.
self.fitness = 0;
value = 0
for i in range(SIZE):
value += self.genes[i]*pow(2,SIZE-1-i)
self.fitness = value
return self.fitness4. 부모 개체 선택 -> 확률 돌림판
# 선택 연산
def select(pop):
max_value = sum([c.cal_fitness() for c in population])
pick = random.uniform(0, max_value)
current = 0
# 룰렛휠에서 어떤 조각에 속하는지를 알아내는 루프
for c in pop:
current += c.cal_fitness()
if current > pick:
return c5. 교차 연산자 -> 새로운 개체 생성
# 선택과 교차 연산
for _ in range(POPULATION_SIZE//2):
c1, c2 = crossover(population);
new_pop.append(Chromosome(c1));
new_pop.append(Chromosome(c2));
# 교차 연산
def crossover(pop):
father = select(pop)
mother = select(pop)
index = random.randint(1, SIZE - 2)
child1 = father.genes[:index] + mother.genes[index:]
child2 = mother.genes[:index] + father.genes[index:]
return (child1, child2)교차 연산자 : 두 염색체에 교차 위치를 선택하여 첫 번째 염색체에서 한 부분을 복사하고, 두 번째 염색체에서 나머지 번호를 순서대로 가져와서 비어있는 부분을 채우는 순서화 교차(ordered crossover) 연산자
# 교차 연산
def crossover(pop):
parent1 = select(pop)
parent2 = select(pop)
pt1 = random.randint(1, 3) # crossover point 1
pt2 = random.randint(4, 6) # crossover point 2
# print(pt1, pt2)
latter_length = len(parent1.genes) - pt2
prt1_mid = parent1.genes[pt1:pt2]
prt2_mid = parent2.genes[pt1:pt2]
prt1_reordered = parent1.genes[pt2:] + parent1.genes[:pt2]
prt2_reordered = parent2.genes[pt2:] + parent2.genes[:pt2]
prt1_reord_filtered = []
prt2_reord_filtered = []
for i in range(SIZE):
if parent1.genes[i] not in prt2_mid:
prt1_reord_filtered.append(parent1.genes[i])
for i in range(SIZE):
if parent2.genes[i] not in prt1_mid:
prt2_reord_filtered.append(parent2.genes[i])
offspring1 = prt2_reord_filtered[-pt1:] + prt1_mid + prt2_reord_filtered[:latter_length]
offspring2 = prt1_reord_filtered[-pt1:] + prt2_mid + prt1_reord_filtered[:latter_length]
return (offspring1, offspring2)
6. 돌연변이 연산자
# 돌연변이 연산
def mutate(c):
for i in range(SIZE):
if random.random() < MUTATION_RATE:
if random.random() < 0.5:
c.genes[i] = 1
else:
c.genes[i] = 0
-- 함수 최적화 --
라그랑주 함수 쓰기 !!
-- 지식 표현 --
데이터[아직 가공 x, 오류 있음] -> 정보[가공] -> 지식[분석/이해] -> 지혜[통찰]
지식 : 암묵지/형식지, 절차적/선언적, 정형화된 형태로 표현
-- 규칙 --
조건부의 지식
예: 신호등이 녹색일 때는 건널목을 안전하게 건널 수 있고, 빨간색일 때는 길을 건너지 말아야 한다
우리가 흔히 아는 지식임. 정형화된 형태로 표현하면?
IF trafficLight = green THEN action = cross
IF trafficLight= red THEN action = stop
인과관계 / 추천 / 지시 / 전략 / 휴리스틱 에 응용함.
-- 프레임 --
슬롯의 집합으로 지식을 표현함.
슬롯 : 이름/값[패싯, 데몬] 형태임
패싯 [value, data-type, dafault, require]
데몬 : [조건임]
(frame
(frame-name Computer)
(frame-type class)
(CPU (default Intel)
(data-type string)
(require (Intel AMD ARM SPARC)))
(OS (default Windows)
(data-type string)
(memory (data-type integer))
(warranty (default 3years)
(HDD (default 1TB))
(price (data-type integer))
(stock (default in-stock)))
(frame
(frame-name Ultra-Slim-Notebook)
(frame-type instance (class Computer))
(CPU (value ARM))
(OS (value Android))
(memory (value 4G))
(HDD (value 512GB))
(price (if-needed look-up-the-list)
(stock (if-needed ask-for-vendor)))
규칙을 사용 -> 조건적인 지식 표현 ->
데몬에 규칙 사용, 규칙의 조건부나 결론부에 프레임 사용
객체 표현에 프레임 사용
정보은닉 아님, 자동으로 호출되는 데몬 개념임.
대상에 대해 갖는 지식의 표현을 목표로 함.
-- 논리 --
[조랑이와 쫑긋이]
[논리 융합]
[CNF]
[타당/ 충족]
[wff]
[논리적 귀결]
[추론 규칙]
[정당성, 완정성]
[논리 융합 반박]
[술어논리] : 서술에 가져서 관계를 기술함.
[존재 한정사 / 전칭 한정사]
[일차술어논리 / 고차술어논리] : [변수뿐만 아니라 함수나 술어 기호도 한정사 가능]
[단일화]
[스콜렘 함수]
-- 의미망 --
is-a(조류, 동물)
is-a(포유류, 동물)
has-a(동물, 피부)
has-a(피부, 벼룩)
has-a(동물, 벼룩)
can(펭귄, 수영)
is-a는 계층 관계, 상속할 수 있음 추이적 관계 만족
has-a는 part-of의 역관계, 상속아님, 대상이 같아야 함. 동호회, 다리 예시
can(조류, 알 낳기) ^ is-a(조류, 펭귄) -> can(펭귄, 알 낳기)
상속이니까 가능
[디폴트값으로 추론하기]
[철수-영희 반지]
[의미망과 프레임의 변환]
의미망 직관적이고 추가 변경 쉬워 하지만 많이지면 복잡해, 통일성 부족해, 재사용 공유 잘 안 돼
-- 스크립트 --
전형적인 상황 -> 절차적 지식, 시간 순서 고려
스크립트 이름
트랙
역할자
자산
진입조건
장면 1:입장, 2, 3, 4:퇴장
결과 조건
-- 온톨로지 --
지식 공유 재사용하게 해당 영역의 개념/ 관계 / 어휘 정의 -> 지식 표현
rdf : 자원에 대한 메타 데이터를 기술 명세
주어 서술어 목적어로 파악함.
<?xml version="1.0"?>
<rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#"
xmlns:contact="http://www.w3.org/2000/10/swap/pim/contact#">
<contact:Person rdf:about="http://www.abc.org/People/EM/contact#me">
<contact:fullName>홍길동</contact:fullName>
<contact:mailbox rdf:resource="mailto:kdhong@abc.org"/>
<contact:personalTitle>부장</contact:personalTitle>
</contact:Person>
</rdf:RDF>
http://www.abc.org/People/EM/contact#me, http://www.w3.org/2000/10/swap/pim/contact#fullName, “홍길동”
http://www.abc.org/People/EM/contact#me, http://www.w3.org/2000/10/swap/pim/contact#mailbox,
mailto:kdhong@abc.org
http://www.abc.org/People/EM/contact#me, http://www.w3.org/2000/10/swap/pim/contact#personalTitle, “부장”
http://www.abc.org/People/EM/contact#me, http://www.w3.org/1999/02/22-rdf-syntax-ns#type,
http://www.w3.org/2000/10/swap/pim/contact#Person
이런식으로 사용함.
시맨틱 웹 : rdf 사용
의미망과 온톨로지 -> 그래프 구조 지식 모델링
온톨로지 -> 공유 , 상호 운영성, 정보및 지식 재사용에 관심있음