| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- Python
- 파이썬
- BOJ
- 9020
- 기계학습
- 설정
- 1101
- 4948
- 15649
- 파이싼
- 1002
- pyenv
- n과 m
- end to end
- 실버
- 밑바닥부터 시작하는 딥러닝
- streamlit
- Mac
- 가상환경
- 백트래킹
- N-Queen
- 경사하강법
- 손실함수
- 그리디 알고리즘
- 개발환경
- 재귀
- 백준
- 신경망 학습
- Today
- Total
파이톨치
[시스템 프로그래밍] Bits, Bytes, and Integers 본문
# 비트로 정보를 표현하기
우리가 배우는 것은 컴퓨터이고 모든 것은 비트 단위로 연산이 이루어 진다.
컴퓨터는 0과 1로 제어된다. 0일 때는 전류를 흘리지 않고 1일 때는 일정한 전류를 흘린다.
왜 비트를 쓰냐면?

부정확하고 노이즈가 있는 상태에서도 안정적으로 정보를 보낼 수 있어서 이다.
우리가 이진법이라고 부르는 것이 비트 연산이다.
예를 들어서 10진법 15213은 2진법에서 11101101101101로 표현된다.
# Encoding Byte Values
Byte = 8 bits
8비트는 1바이트이다.
1바이트가 표현할 수 있는 범위는 그러면 00000000에서 11111111까지가 된다.
# Boolean Algebra
Boolean Algebra는 논리 연산자로 이루어져 있다.
And, Or, Not, Xor이다.
| x | y | & (AND) | | (OR) | ~ (NOT) | ^ (XOR) |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
연산은 다음과 같이 진행이 된다.
모든 연산을 다음 4 연산자로 해결할 수 있다.
비트 연산자를 사용하면 swapping을 간단하게 구현할 수 있게 된다.
void inplace_swap(int *x, int *y) {
*y = *x ^ *y;
*x = *x ^ *y;
*y = *x ^ *y;
}다음과 같이 하면 swap을 진행할 수 있다고 한다.
^ 는 XOR 연산자이다.
잘~~ 생각해보자. *a ^ *a = 0이다. 왜냐하면 같으면 0 이니까 이다. 또 0 ^ *a = *a 이다.
두번째 줄을 바꿔 쓰면, *x = *x ^ *x ^ *y 이다. 그러면 결과적으로 x에 y값이 저장된다.
그러면 세번째 줄에서 *y ^ (*x ^ *y) 가 되고 연산자의 순서를 바꿔주면 *x ^ (*y ^ * y)가 된다.
이런 과정으로 swap을 할 수 있게 되는 것이다.
# Representing & Manipulating Sets
비트로 재밌는 연산을 할 수가 있다.
[7, 6, 5, 4, 3, 2, 1, 0] 과 같은 리스트가 있다고 생각해보자.
{0, 3, 5, 6}을 리스트에서 뽑는 상황에서
[0, 1, 1, 0, 1, 0, 0, 1] 다음과 같이 표현을 할 수 있다.
0은 안 뽑는 것이고, 1은 뽑는 것이다.
{0, 2, 4, 6}은 [0,1, 0, 1, 0, 1, 0, 1]이다.
다음과 같이 표현을 했을 때 다음과 같은 표를 만들 수 있다.
| 연산자 | 기능 | 비트 결과 | 집합 결과 |
| & | 교집합 | 01000001 | {0, 6} |
| | | 병합 | 01111101 | {0, 2, 3, 4, 5, 6} |
| ^ | 대칭 차집합 | 00111100 | {2, 3, 4, 5} |
| ~ | 보수 | 10101010 | {1, 3, 5, 7} |
참고로 보수는 단항 연산자라서 {0, 2, 4, 6}의 보수를 결과로 나타낸 것이다.
# Bit - Level Operations in C
C언어에 &&, || 연산자가 있는데 이것들은 논리 연산자이지 비트 연산자가 아니니까 착각하지 말아야 한다.
&, |, ~, ^와 같이 표현하면 생각한 대로 될 것이다.
3을 2진법으로 표현을 해보면 0000 0011이다.
num = 3; num << 3 의 결과는 0001 1000이 된다 이는 24라는 결과가 나온다.

Logical shift : 0으로 채우기
Arithmetic shift : 가장 중요한 비트 복제하기
# Two's Complement Values / Numeric Ranges
2의 보수법은 간단하게 00000000 00000000 의 공간이 있을 때 가장 큰 값을 음수로 설정하는 것이다.
10000000 00000000 의 값은 -1 * (2 ** 15) 이다.
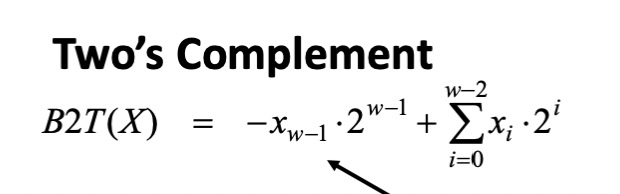
그리고 나머지 자리는 그냥 +로 연산하는 것이다. 이런 식으로 생각을 해보면 음수를 표현 할 수 있는 것이다.
그러면 2의 보수법은 -1 * (2 ** (w-1))까지 표현 가능 한 것이고, 최대로는 2 ** (w-1) -1 만큼의 표현이 가능한 것이다.
만약 제일 큰 값을 음수로 설정하지 않는다고 가정하면 0 ~ 2 ** w -1 까지의 범위로 표현이 가능할 것이다.
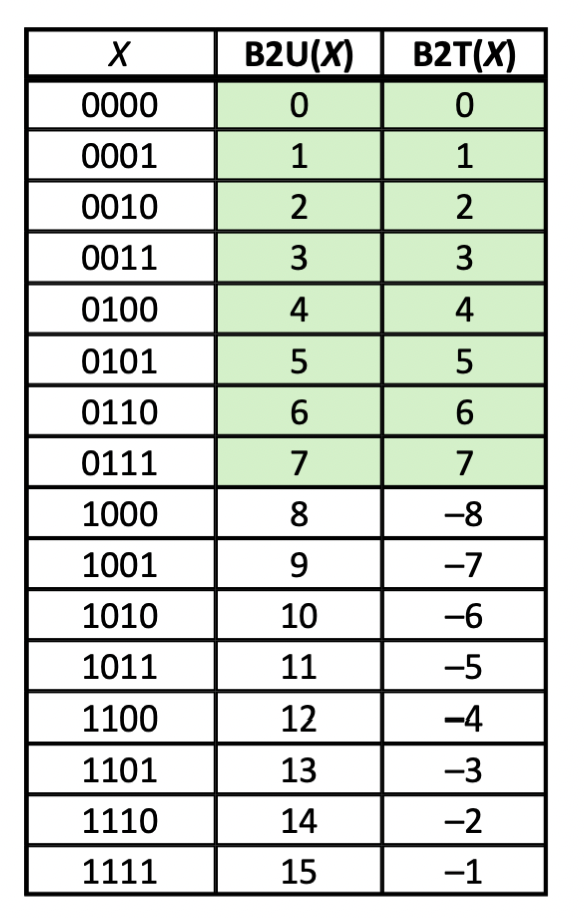
가령 4비트 짜리 연산이라면 다음과 같은 방식이라고 볼 수 있다.
# Conversion, Casting
Unsigned 는 양수만 나타내는 표현이다. 그렇다면 Signed는 양수와 음수 모두를 표현할 수 있는 수이다.
앞에서 했던 2의 보수법이 Signed를 나타내는 것이다. 하지만 이것들은 서로 변환할 수 있다고 한다.
2의 보수법을 Unsigned로 바꾸는 방법은 다음과 같다.
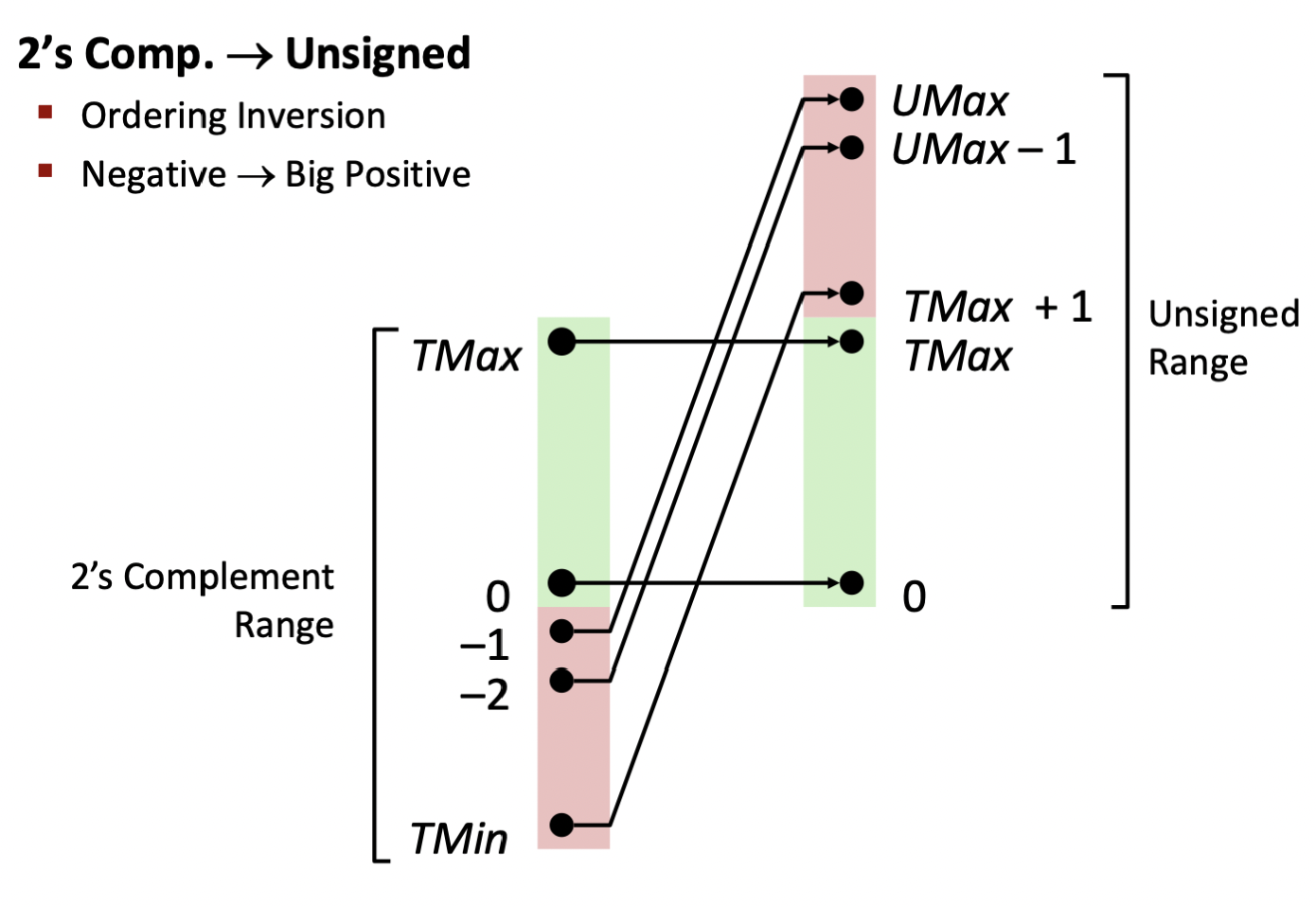
음수에 있는 것을 위로 올려버리는 것이다. 그렇게 큰 양수로 만든다.
정수의 기본은 Signed이다. 하지만 의도적으로 Unsigned로 만들어 줄 수 있다.
0U, 4141U와 같은 식으로 U를 붙여주면 된다.
또한 Casting을 통해서 위의 작업을 해줄 수 있다.
int tx, ty;
unsigned ux, uy;
// Explicit casting
tx = (int) ux;
uy = (unsigned) ty;
// Implicit casting
tx = ux;
uy = ty;
둘은 같은 표현이지만 이를 표시해주냐 아니냐가 다르다. 왼쪽에 있는 데이터 타입에 맞게 변하는 모양이다.
두개의 표현이 섞여 있으면 Signed가 Unsigned로 변환된다.
Word = 32라면, TMIN = -2,147,483,648 , TMAX = 2,147,483,647 가 된다.
# Sign Extension
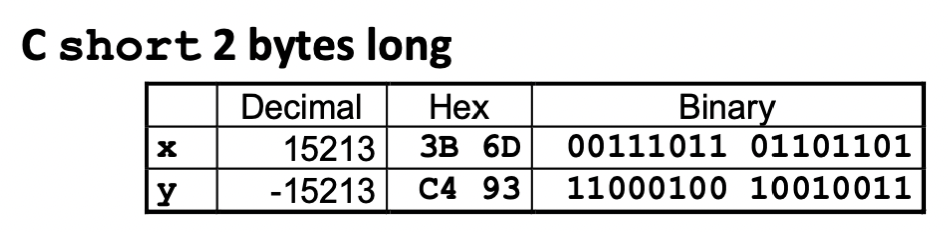
short int x = 15213;
int ix = (int) x;
short int y = -15213;
int iy = (int) y;다음과 같이 더 큰 수로 Casting할 때 규칙이 있다.
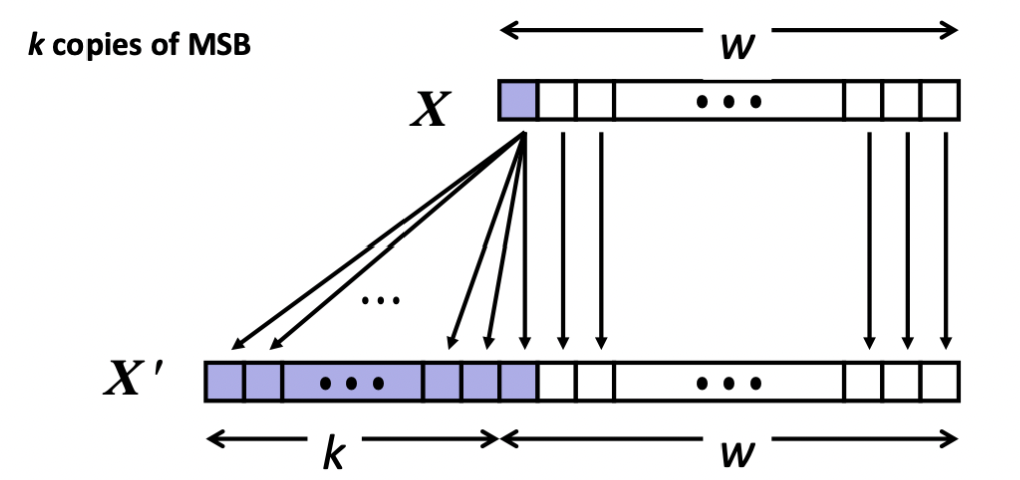
다음과 같은 형식으로 맨 앞에 있는 0 또는 1이 복사되어 들어간다.
이는 컴파일러에서 자동으로 수행하는 것이다.
# Unsigned Addition
음이 아니 수 x와 y가 있고 범위는 0 ~ 2 ** w - 1 이다.. 이 수들은 w개의 비트로 표현할 수 있다 (unsigned 일 경우).
만약 더하게 된다면 가능한 범위는 0 ~ 2 ** (w+1) - 2일 것이다. 이것을 표현하려면 w+1 개의 비트가 필요하다.
더하기를 할 때마다 비트를 하나씩 더 추가해 준다면 비효율적일 것이다. 때문에 다음과 같은 연산을 한다고 한다.
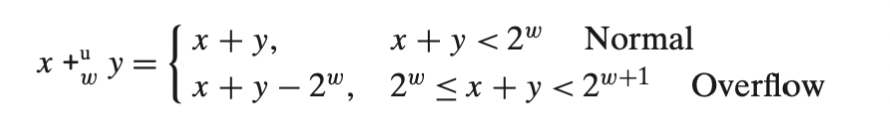
이해 하기 쉽게 말로하자면 넘어가면 0부터 시작하라는 것이다.
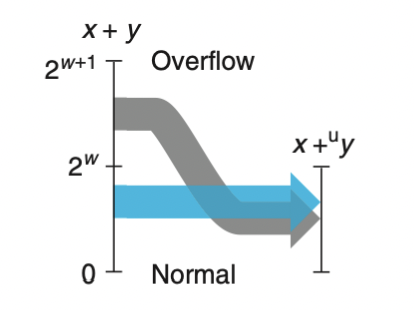
결국 넘어가든 넘어가지 않던 제한된 word 사이즈에 담아야 하기 때문에 다음과 같은 방식으로 하는 것인데,
내가 궁금한 것은 넘어간지 안 넘어간지 어떻게 구분하는가 이다.

다시 한번 천재들의 아이디어에 감탄했다. 간단한 방법이었다.
더하면 커져야 하는데 더했을 때 기존의 수들보다 작아지면 넘어서서 자른 것이다.
# Two's Complement Addition
이것은 우리가 일반적으로 사용하는 더하기 연산일 것이다. 이것도 마찬가지로 오버플로우가 발생할 것이다.
int s, t, u, v;
s = (int) ((unsigned) u + (unsigned) v);
t = u + v;일 경우에 s == t 라는 결과가 나온다.
다만, 오버플로우가 발생할 때 양쪽으로 넘겨준다는 특징이 있다.
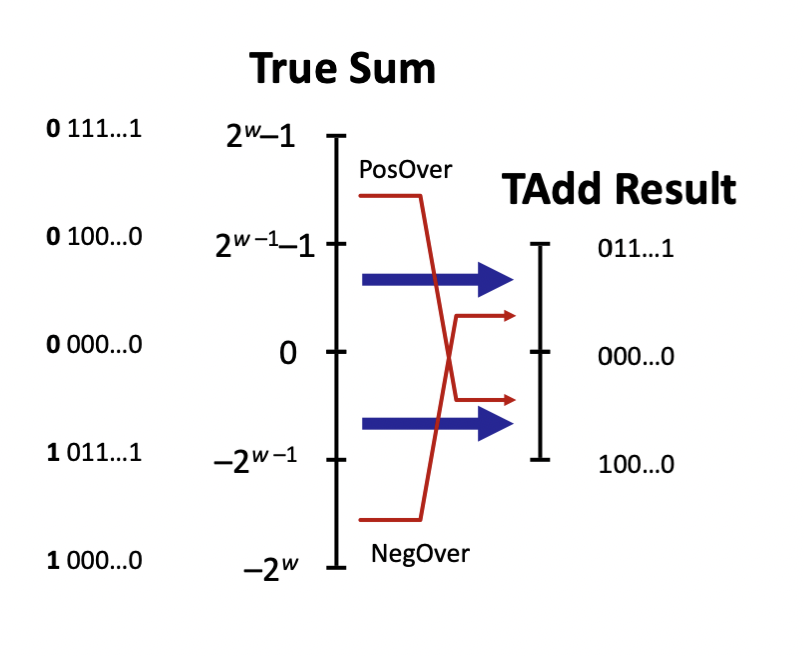
# Unsigned Multiplication
일단 범위부터 생각을 해보면 0 <= x, y < 2 ** w - 1 이다.
그렇다면 x * y 의 범위는 0 ~ 2 ** 2w - 2 * (w+1) + 1이 된다. 이 때 오버플로우가 발생하게 된다면 모듈로 연산으로 떨군다.
( x * y ) mod 2 ** w 로 값을 떨구면 된다.
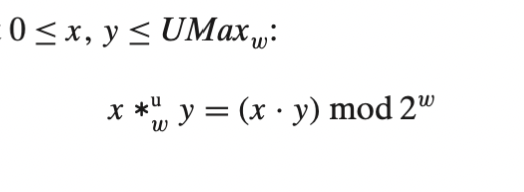
'대학수업' 카테고리의 다른 글
| [인공지능] 정보 이용 탐색 (휴리스틱 탐색) (1) | 2022.09.15 |
|---|---|
| [시스템 프로그래밍] Representations in memory, pointers, strings (0) | 2022.09.15 |
| [확률과 통계] 기술 통계(Descriptive Statistics) (0) | 2022.09.09 |
| [웹 프로그래밍] HTML이란? (2) | 2022.09.08 |
| [인공지능 개론] 인공지능이란 무엇일까? (0) | 2022.09.05 |




